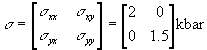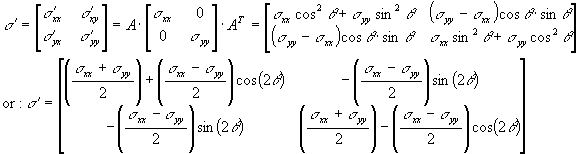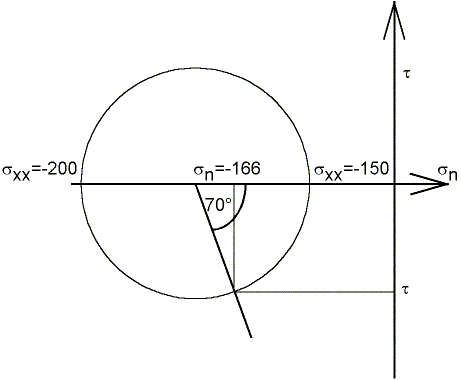12.520 Geodynamics

Problem set 1

Problem 2 (10%)Turcotte & Schubert, 2-12 (Recall that T&S use a different sign convention for compressive stress)

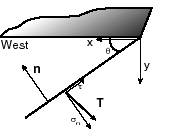
The state of stress at a point on a fault is is s_yy = 150 MPa, s_xx = 200 MPa, and s_xy = 0 (y is depth, and the x axis points westward). What are the normal stress and the tangential stress on the fault plane if the fault strikes N-S and dips 35° to the west?

Solution:
There are at least three methods to solve the problem. Some considered the equilibrium of a prism defined between the fault and the surface, which is fine, but is equivalent of redemonstrating some relations in class (or in question 1) for the particular porblem in this question. This is combersome and "dangerous'. I prefer to expend on use some laws shown in class, and illustrate their use through this problem. You should all be able to jongle between the conventions and units. Also, note that using the normal to the fault plane in the upward or downward direction should not influence the result.

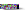I. Use the definition of the traction vector for an arbitrary plane:

The 2-D stress tensor is:

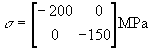The normal vector for the fault plane is:

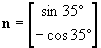The traction vector T for the plane with normal n is:

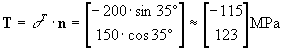
The coordinates of this vector are in the (x,y) coordinate system.

The projection of T on the n-direction is the normal stress on the fault plane:

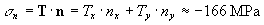
The projection of T onto fault plane is the shear stress (tangential):

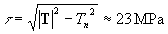
II. Rotation of the coordinate system

Since the problem is 2D, the stress tensor is:

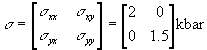
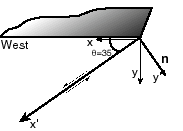To determine the stresses on the fault plane, we rotate the coordinate system from (x',y') to (x,y) by an angle of 35º (positive clockwise).

The rotation matrix A is: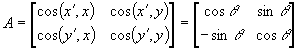

and the new stress tensor is:

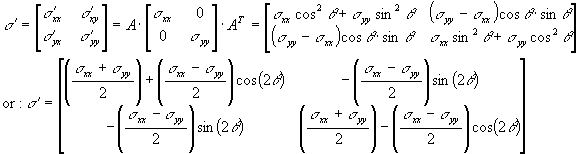
(the second expression may remind you of the Mohr circle. Check the third solution!)

Substituting the stress values: 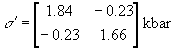, where:

_ the normal stress on the fault plane is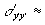

1.66 kbar, and

_the shear stress (tangential) is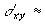

-0.23 kbar. The magnitude is still 23 kbar. the negative sign gives the direction of shear.

Note: in this problem the notation of T&S was used (for compression as a positive value), and we sued kbars. That shouldn't bother anybody, does it?

III. Mohr's circle: the original stress tensor is diagonal, meaning that we are in the principal set of coordinates. The most compressive stress is -s_xx=-200 MPa, and the least compressive stress is -s_yy=-150 MPa. Graphically, take the angle 2×35°=70° anticlockwise from t_yy, and read: s_n=-166 MPa, t=-23 MPa.

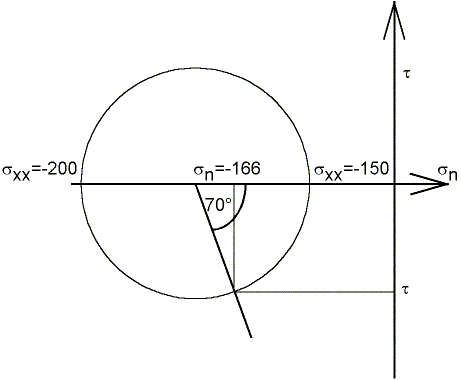A note on the sign convention: your favorite TA uses the following "trick": I always turn the same direction (clockwise) and go from n to n, passing by a stress direction, say that of s_yy So, I turn in the geometrical space clockwise by q, arrive in the direction of s_yy, Now, I am in the stress space, and I rotate2q , still clockwise. Check that I have the right result, according to the more usual change of definition. (and tell me if it doesn't work, please).

Previous | back | next problem