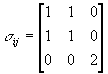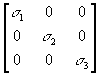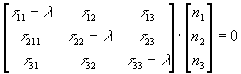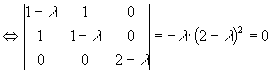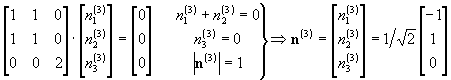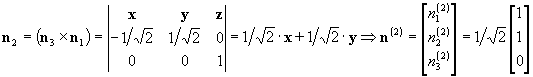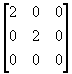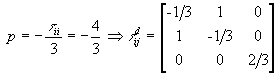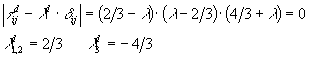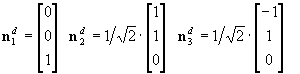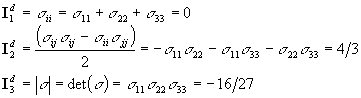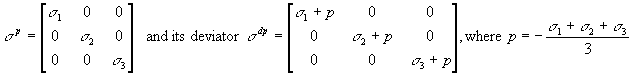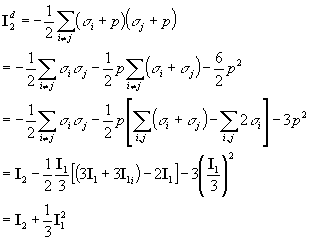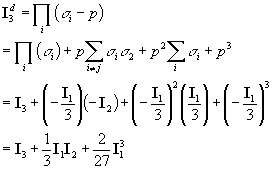12.520 Geodynamics
Problem set 1
 Problem
4 (40%)
Problem
4 (40%)
For the stress tensor:
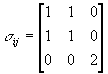 a) Find the principal stresses and directions.
(Be sure that your principal coordinate system is right-handed)
a) Find the principal stresses and directions.
(Be sure that your principal coordinate system is right-handed)
b) Calculate the three invariants for this stress
tensor and for the associated principal stress tensor and compare their
values.
c) Find the deviatoric stress tensor sijdev
d) Find the principal stresses and directions of
the deviatoric stress tensor. Find the invariants of the deviatoric stress
tensor.
e) What are the relations of the principal stresses,
directions, shear, invariants, etc. for these tensors (the complete and
deviatoric tensors invastigated above)? Can you anything in general about
these relations for an arbitrary tensor and its deviator ?
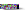 Solution:
Solution:
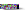 a) The principal
stresses form a diagonal stress tensor of the form:
a) The principal
stresses form a diagonal stress tensor of the form:
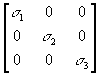
If n is a principal direction, and l
is its associated principal stress, the following equation is true:
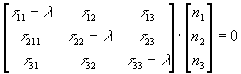
or, in index notation: 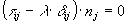
This equation has a solution only if: 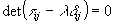
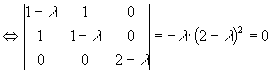
Hence: l=2, 2, or 0
_ Two conditions are imposed on the principal vectors
as a convention:
1) They must be normalized: 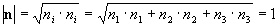
2) They constitute a right-handed coordinate system:

The direction associated with s3=0
is uniquely defined. We only have an uncertainty on the direction. For
instance, we chose:
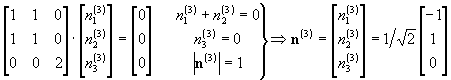
The two other principal values are equal but different
from s3.
The directions associated with them are not uniquely determined, but define
a plane on which any two perpendicular directions can be selected, as long
as the system is right-handed. We decided to impose n1=0 for the direction
associated with s1=2.

Finally, we calculate n2 to make a right-handed
system. Verify that is indeed a principal direction, with principal value
s2=2.
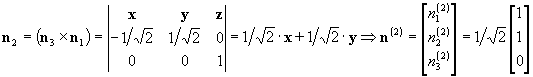
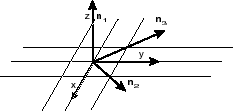
Let's draw a picture of the coordinate system and principal
axes :
both of them are right-handed.
 b) By definition,
invariants do not change under rotation of the coordinate system. Since
the principal stress tensor is the original tensor rotated into different
coordinate system, their invariants must be the same. It's easier to calculate
invariants for the tensor in the principal axis frame. But you should obey
the problem set, and check the invariance by calculating the invariants
for both the principal and original stress tensors
b) By definition,
invariants do not change under rotation of the coordinate system. Since
the principal stress tensor is the original tensor rotated into different
coordinate system, their invariants must be the same. It's easier to calculate
invariants for the tensor in the principal axis frame. But you should obey
the problem set, and check the invariance by calculating the invariants
for both the principal and original stress tensors
| |
principal stress tensor
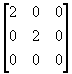
|
original stress tensor

|
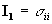
|
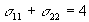
|
4
|
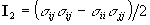
|
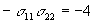
|
-4
|
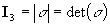
|
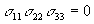
|
0
|
 c) The deviatoric
stress tensor is obtained by substracting the (isotropic) pressure:
c) The deviatoric
stress tensor is obtained by substracting the (isotropic) pressure:
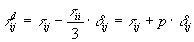
where pressure is: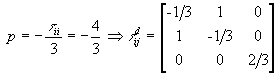
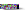 d) following
the procedure descried in a), we can find out that
d) following
the procedure descried in a), we can find out that
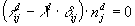
under the condition of: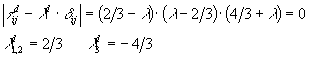
and principal directions are:
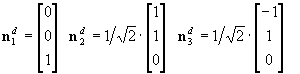
the invariants are: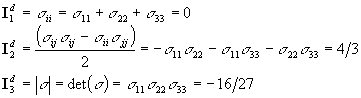
 e) As we have
seen, the principal stress directions for a stress tensor and its deviator
are the same. The principal stress themselves, however, are different because
we have removed the pressure from the deviatoric stress tensor. Thus, the
principal stresses of the deviator are simply the sum of the original principle
stresses and the pressure:
e) As we have
seen, the principal stress directions for a stress tensor and its deviator
are the same. The principal stress themselves, however, are different because
we have removed the pressure from the deviatoric stress tensor. Thus, the
principal stresses of the deviator are simply the sum of the original principle
stresses and the pressure: 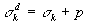 where
where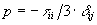 .
.
Thus, for an arbitrary stress tensor and its deviator,
we have:
principal stresses 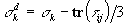
principal directions 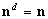
shear stresses are the same 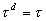
invariants 
The relationships between invariants can be proved by considering
the invariants of a principal stress tensor:
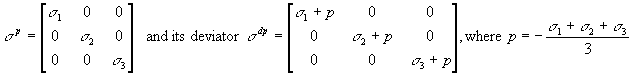
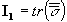
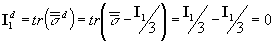
![]() Problem
4 (40%)
Problem
4 (40%)